Educational Codeforces Round 153 A-E (博弈论 DP 拆点)
A. Not a Substring
给一个仅由
(和)组成的字符串,它的长度为 。要求构造一个长度为 的新字符串 ,且 不是 的连续子串。输出新字符串 。
构造
很明显一个字符串如果是 (((()))) 的子字符串,那它一定不是 ()()()() 的子字符串。因此只需要构造出两个字符串进行判断即可。
void solve() { std::string s; std::cin >> s; std::string s1, s2; rep(i, s.size()) { s1 += "()"; s2 += "("; } rep(i, s.size()) { s2 += ")"; }
if (s1.find(s) == std::string::npos) { std::cout << "YES\n" << s1; } else if (s2.find(s) == std::string::npos) { std::cout << "YES\n" << s2; } else { std::cout << "NO"; }}B. Fancy Coins
Monocarp 要进行一项价值 的支出。他现在有两种价值的硬币:
- 价值为 的普通硬币 枚和同价值的花式硬币无限枚
- 价值为 的普通硬币 枚和同价值的花式硬币无限枚
Monocarp想要恰巧支付 并花费尽可能少的花式硬币。输出消耗的花式硬币的数量。
贪心
很明显我们要尽可能使用价值为 的硬币,少量价值为 的硬币只是拿来凑零的。我们可以将 枚价值为 的普通硬币看作 枚价值为 的普通硬币,接下来只需要花费 枚价值为 的硬币和 枚价值为 的硬币,简单的进行减法即可得到答案。
void solve() { int m, k, a, b; cin >> m >> k >> a >> b;
int mk = m % k; int m_k = m / k; if (a >= mk) { a -= mk; b += a / k; cout << std::max(0, m_k - b); } else { cout << std::max(0, m_k - b) + mk - a; }}C. Game on Permutation
Alice 和 Bob 正在玩一个游戏。
游戏进行在一个大小为 的排列上。两人轮流在序列上选数,选择的数必须满足其大小的下标都小于上一个人选择的数的大小和下标,最后不能行动的人赢。
Alice 先手。问 Alice 先选择哪个数,后续一定存在必胜。输出这种数的数量
博弈论
很明显这是一个 Anti-Game。由 SJ 定理可知,这个游戏的 PN 态等价于它的相反游戏(即不能行动的人输)。我们只需要获取排列中原游戏每个数的 PN 态,最后统计 P 态的数量即可。
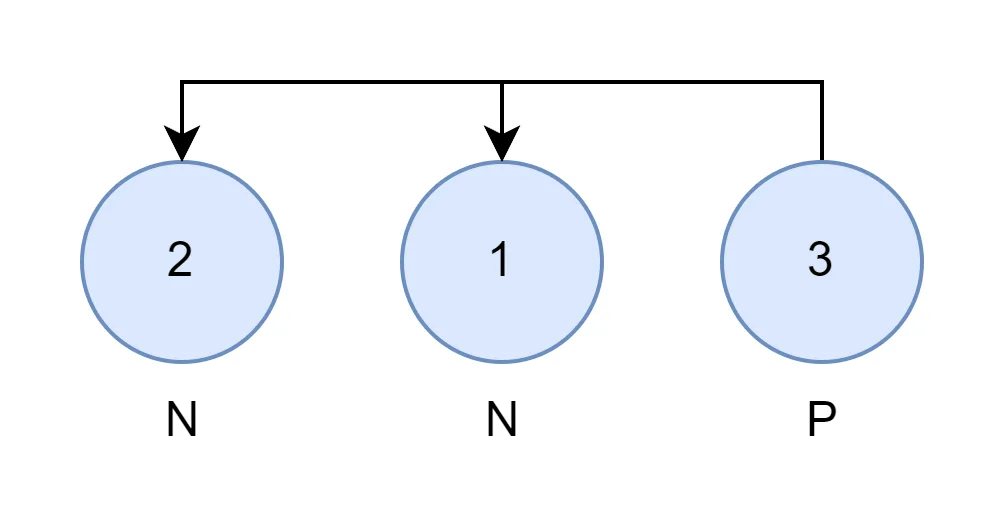
对于样例1,当选择 和 后,下一个人均不能行动,因此为 N 态,而 只能转移到 或者 这两个 N 态,因此为 为 P 态。最终答案为 1
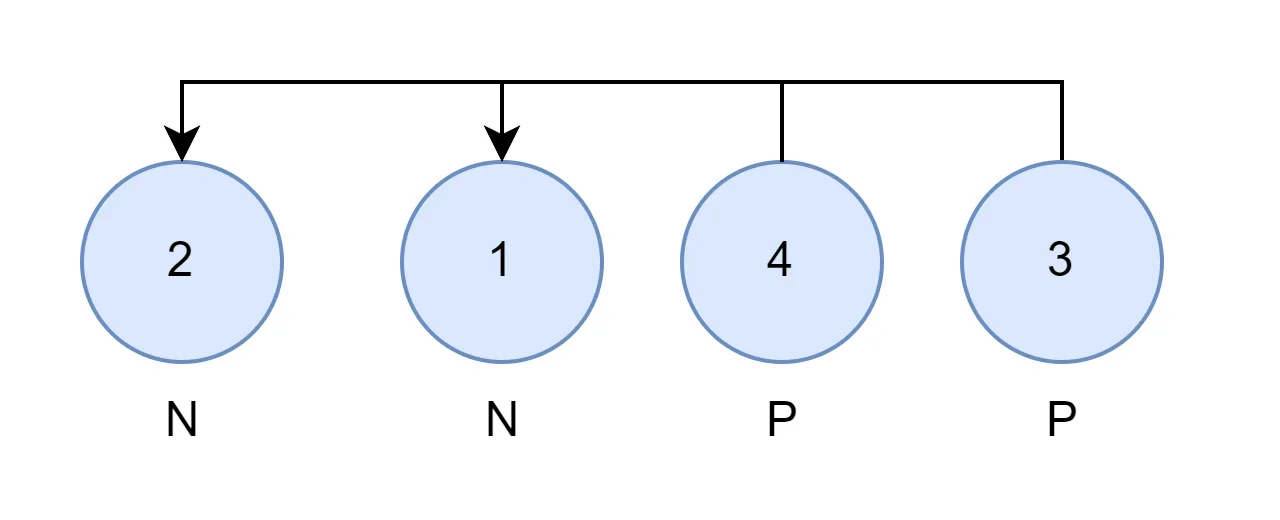
对于第三个样例同理,由于 和 只能转移到 和 ,因此答案为
在实现时,只需要从头开始遍例第 个数,判断前面比 小的数中是否存在 P 态,如果存在则 为 N 态,否则为 态。这可以使用树态数组实现,这里白嫖一下 pbds。
#include<ext/pb_ds/tree_policy.hpp>#include<ext/pb_ds/assoc_container.hpp>void solve() { int n; read(n); std::vector<int> s(n); reads(all(s));
using namespace __gnu_pbds; tree<int, null_type, std::less<int>, splay_tree_tag, tree_order_statistics_node_update> N, P;
for (int i = 0; i < s.size(); i++) { int nNum = N.order_of_key(s[i]); // 比 s[i] 小的数中有几个 N 态 if (nNum == 0) { // 刚开始第一个数 N.insert(s[i]); } else if (N.size() + (P.size() - P.order_of_key(s[i])) == i) { // N 态的数量加上能不能转移到的 P 态的数量等于当前下标 // 即不能转移到 P 态 P.insert(s[i]); } else { N.insert(s[i]); } } std::cout << P.size();}D. Balanced String
输入一个 01 串 ,进行尽可能少的交换其中的
0和1,使交换后新字符串中的子串01和10的数量相同。输出最少的交换次数
DP
参考了 jiangly 的代码
考虑使用 DP 时依次向第 位放置 0 或者 1,因此我们需要两个状态表示当前位数和放了多少 1。由于最终答案是最少的交换次数,目标是使 01和10串的数量相等,所以我们还需要一个状态去表示 01 串的数量,但由于在放 1的过程中除了形成 01 串还会形成 11 串,这在 DP 时难以记录,因此可以直接去表示 01 和 11 的数量。最终我们将状态定义为
-
表示当前位数
-
表示当前放
1的数量 -
表示当前
01串和11串的数量
他们之间的状态转移可以是:
-
: 当前位置放 0
-
:当前位置放 1,原字符串位置为 1,不需要交换
-
: 当前位置放 ,原字符串位置为 1,需要进行交换
可以看出这个状态转移非常像 01背包,因此我们可以采用相同的方式进行去掉 这一维。
但要进行 DP,我们还需要得知最终 01 和11 串的数量,即 的上限。
考虑原字符串中的子串有 01,10,11和00 四种,其中00和11无论怎么交换数量都不会变。因此我们可以统计出 中 1和0 的数量,算出 00 和11的数量。
对于最终交换成的新字符串 01 串的数量和 10 串的数量是相同的,因此可以算出最终字符串中 01 串和 10 串的数量,进而可以算出 01 和 11 的数量为
那么现在可以实现代码了
const int maxn = 117;int dp[maxn][maxn * maxn / 2];void solve() { std::string s; std::cin >> s; int c = s.size(); int c1 = std::count(all(s), '1'), c0 = std::count(all(s), '0'); int need = (c * (c - 1) / 2 - c0 * (c0 - 1) / 2 + c1 * (c1 - 1) / 2) / 2; std::memset(dp, 0x3f, sizeof(dp)); dp[0][0] = 0; for (int i = 0; i < c; i++) { for (int j = std::min(c1, i+1); j >= 1; j--) { for (int k = i; k <= need; k++) { dp[j][k] = std::min( dp[j][k], dp[j - 1][k - i] + (s[i] == '0') ); } } } std::cout << dp[c1][need];}E. Fast Travel Text Editor
给一串仅由小写字母组成的字符串 。现在在两个字符中间有一个光标,光标不会出现在字符串的最左侧或者最右侧。
光标可以进行两种操作
- 左移/右移一位,代价为 1
- 跳转到其他左右字符相同的位置,代价也为 1
有 次询问,每次询问从光标从第 个位置到第 的位置最小的代码
图论 拆点 01最短路
首先第一反应是建图bfs
如果朴素建图,最坏情况下 可能全是一样的字符,时间复杂度 ,这显然是不可接受的。但是由于光标可以跳转到和其他所有左右字符相同的位置,可以进行拆点操作。

拆点方式如图,对于左右两字符相同的地点,建立一个中转点,入边边权为 ,出边为 。建图后进行 最短路即可。
对于每次从 到 ,它如果经过中转点,那么距离一定是 。如果它不经过中传点,那么距离是 。通过这种方式可以有效减少 BFS 的次数。
const int N = 5e4+5;const int M = 28;
int id[M][M][2]; // 中转点的编号std::vector<std::pair<int,int>> G[N*2+17];
std::vector<int> dis[M][M];std::deque<int> q;
void add_edge(int u,int v,int w){ G[u].push_back({v,w}); G[v].push_back({u,w});}
int main(){ std::string s; std::cin >> s; int n= s.size(); for(int i=0;i<n;i++)s[i]-='a';
// 建立所有的中转点 int cnt=n-1; for(int a=0;a<26;a++){ for(int b=0;b<26;b++){ id[a][b][0] = cnt++; id[a][b][1] = cnt++; G[cnt-2].push_back({cnt-1,1}); } } for(int i=0;i<n-2;i++){ add_edge(i,i+1,1); } for(int i=0;i<n-1;i++){ G[i].push_back({id[s[i]][s[i+1]][0],0}); G[id[s[i]][s[i+1]][1]].push_back({i,0}); }
for(int a=0;a<26;a++){ for(int b=0;b<26;b++){ // 从中转点的出点开始 0-1 BFS dis[a][b] = vector<int>(cnt,1e9);
auto& d = dis[a][b]; int st = id[a][b][1]; d[st]=0; q.push_back(st);
while(q.size()){ int u=q.front();q.pop_front(); for(auto [v,w]:G[u]){ if(d[u]+w<d[v]){ d[v]=d[u]+w; if(w==0) q.push_front(v); else q.push_back(v); } } } } }
int query; read(query); while(query--){ int l,r; read(l, r); l--,r--; int ans = abs(r-l);
for(int i=0;i<26;i++){ for(int j=0;j<26;j++){ ans = min(ans,dis[i][j][l]+dis[i][j][r]+1); } } std::cout << ans; } return 0;}