Mslxl's Blog

Integrate Life

2020-2021 ACM ICPC Asia Nanjing Regional Contest

发布于 # Competitive Programming # ICPC

题目链接

官方题解

A - Ah, It’s Yesterday Once More

构造一张二维地图，仅有墙壁和空白组成。在每个空白处都有一个人，每个人在接下来的 50000 步中将向一个方向随机移动。 要求构造的地图必须小于 20×2020\times 20，至少有两个空白，每个空白之前必须是相互可达的，不能有环，50000步后所有的人25%25\%的可能性不在同一个格子。

构造

很奇怪的一道题，练习的时候莫名其妙的就 A 了。

由于题目并没有输入数据，所有的人的行动数据都是随机的。很明显按照题目的意思，答案可以是固定的，没必要在程序中生成。而且路线长什么样子没什么关系（因为人的行动完全随机）。 只要保证人尽可能的多，路线尽可能的长就行。

然后在 cf 上交了个 PHP 莫名其妙的就 A 了。

20 20
11111101111101111101
10010110010110010111
01011011011011011001
11101101101101101101
10110110110110110110
11011011011011011011
01101101101101101101
10110110110110110111
10011011011011011001
11101101101101101101
10110110110110110110
11011011011011011011
01101101101101101101
10110110110110110111
10011011011011011001
11101101101101101101
10110110110110110110
11011011011011011011
01001101001101001101
11110111110111110111

D - Drgree of Spanning Tree

给一个无向联通图，有nn个定点mm条边。找到一颗生成树，使得这个生成树的每个顶点的度数不大于n2\frac{n}{2}

注意可能有自环或者重边

图论 并查集 思维 生成树

训练的时候没做出来 现在某种意义上我是抄的这个题解Degree of Spanning Tree

CF上有一道相似的题目（还更麻烦点）Codeforces 1133F2

假如我们现在有这样一张图和它的一个生成树

我们想要降低顶点 11 的度

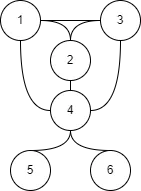
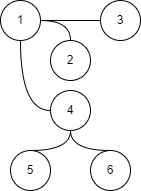
太难看了，我们重新整理一下

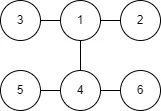
之后我们将11作为根，使用并查集标记它的所有子树

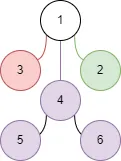
依次遍历原图中所有的边，如果这个边不是和根直接相连的，而且又连接了两个不同的子树，那么我们可以试图将这条边加入生成树中，并移除根与其中一个字树的联系。

这里我们选择(2,4)(2,4)边

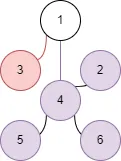
显然，新连接的边的定点不符合题意。我们可以反过来试一下（这里没有这个必要，但是部分情况可能会用到这个操作）

我们连接(2,4)(2,4)时，不再断开(1,2)(1,2)，而是断开(1,4)(1,4)

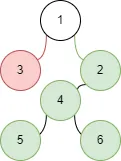
连接(2,4)(2,4)边的两种方式都不符合要求，现在应该恢复到未连接2−42-4前的状态，继续尝试选择其他边

接下来尝试(3,4)(3,4)也不行，直到我们选择(2,3)(2,3)

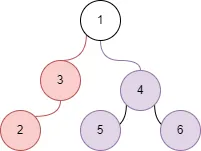
通过这种操作，我们将11的度数降低了11

类似的，这道题我们也可以采用这种方式。树我们可以随便生成一个，而其中度数大于n2\frac{n}{2}的定点只会有一个。

我们只需要将这个顶点作为根，重复上面的操作即可。

// clang-format off
#include <algorithm>
#include <bits/stdc++.h>
using ll = long long; using ul = unsigned long long; using ld = long double;
template <typename T> inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x){ char c;T f=1; while(!isdigit(c=getchar())) if(c=='-')f=-1; x=(c&15); while(isdigit(c=getchar())) x= (x<<1) + (x<<3) + (c&15); x*=f; } template <typename T, typename... A> inline void read(T &value, A &..._t) { read(value), read(_t...); }
void solve(const std::size_t testcase);
#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)
#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)
#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)
#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)
int main() {
  std::size_t t = 1;
  read(t);
  // std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr);
  rep1(i, t) solve(t);
  return 0;
}
// clang-format on


const int maxn = 2e5 + 10;


std::vector<std::pair<int, int>> es;
std::map<std::pair<int, int>, int> mp;


// 存生成树用的()
struct Edge {
  int to;
  int next;
} edges[maxn << 2];


int head[maxn], idx;
int deg[maxn];


void add(int u, int v) {
  edges[idx] = {v, head[u]};
  head[u] = idx++;
  edges[idx] = {u, head[v]};
  head[v] = idx++;
}


int pre[maxn];
int chose[maxn];


// 并查集
int fi(int x) { return x == pre[x] ? x : pre[x] = fi(pre[x]); }


void dfs(int u, int fa, int sig) {
  pre[u] = sig;
  for (int i = head[u]; ~i; i = edges[i].next) {
    int v = edges[i].to;
    if (v == fa)
      continue;
    dfs(v, u, sig);
  }
}


// 多测清数据
void init(int n, int m) {
  mp.clear();
  es.clear();
  for (int i = 0; i <= n; i++) {
    head[i] = -1;
    deg[i] = 0;
    pre[i] = i;
  }


  for (int i = 0; i <= m; i++) {
    chose[i] = 0;
  }
  idx = 0;
}


void solve(const std::size_t testcase) {
  int n, m;
  read(n, m);
  init(n, m);
  for (int i = 0; i < m; i++) {
    int u, v;
    read(u, v);
    if (u > v)
      std::swap(u, v);
    es.push_back({u, v});
  }
  std::sort(es.begin(), es.end());
  es.erase(std::unique(es.begin(), es.end()), es.end()); // 删除重边
  m = int(es.size());
  // 使用并查集建立生成树
  for (int i = 0; i < m; i++) {
    int u = es[i].first;
    int v = es[i].second;
    mp[{u, v}] = mp[{v, u}] = i;
    int fu = fi(u), fv = fi(v);
    if (fu != fv) {
      add(u, v);
      pre[fu] = fv;
      deg[u]++;
      deg[v]++;
      chose[i] = 1;
    }
  }


  // 不连通直接输出 NO
  int flag = 0;
  for (int i = 2; i <= n; i++) {
    if (fi(i) != fi(1))
      flag = 1; // 不连通
  }
  if (flag) {
    std::cout << "No\n";
    return;
  }


  // 如果所有的度数都小于n/2，那么不需要调整，直接输出答案
  int rt = -1;
  for (int i = 1; i <= n; i++) {
    if (deg[i] > n / 2) {
      rt = i;
      break;
    }
  }
  if (rt == -1) {
    std::cout << "Yes\n";
    for (int i = 0; i < m; i++) {
      if (chose[i]) {
        std::cout << es[i].first << " " << es[i].second << "\n";
      }
    }
    return;
  }


  // 以rt为根，将其所有的子树加到一个集合里
  for (int i = 1; i <= n; i++)
    pre[i] = i;
  for (int i = head[rt]; ~i; i = edges[i].next) {
    dfs(edges[i].to, rt, edges[i].to);
  }
  for (int i = 0; i < m; i++) {
    if (chose[i])
      continue; // 这条边在当前生成树中已存在，跳过
    int u = es[i].first, v = es[i].second;
    int fu = fi(u), fv = fi(v);
    if (u == rt || v == rt)
      continue; // 这是和根相连的点，要么已使用，要么添加后会增加度数
    if (fu == fv)
      continue; // 这条边的两顶点同属于一棵子树，使用只会增加度数


    // 用u-v边替换掉rt-fu边
    deg[rt]--;
    deg[u]++;
    deg[v]++;
    deg[fu]--;


    if (deg[u] > n / 2 || deg[v] > n / 2) { // 添加u-v边后，u,v两节点是否不合法
      // 原本从 rt-fv 连接子树，换成 rt-fu
      deg[fu]++;
      deg[fv]--;
      if (deg[u] > n / 2 || deg[v] > n / 2) {
        // u-v 仍不合法，把原来的边恢复，再去尝试另一条连接两颗子树的边
        deg[rt]++;
        deg[u]--;
        deg[v]--;
        deg[fv]++;
        continue;
      } else {
        // u -v 合法，也就是说成功把根的度数降低了1
        pre[fv] = fu;
        chose[i] = 1;
        chose[mp[{rt, fv}]] = 0;
      }
    } else {
      // u -v 合法，也就是说成功把根的度数降低了1
      pre[fu] = fv;
      chose[i] = 1;
      chose[mp[{rt, fu}]] = 0;
    }
    if(deg[rt] <= n/2) break; //如果现在根的度数满足要求，就不需要继续进行了
  }
  if(deg[rt] <= n/2){
    std::cout << "Yes\n";
    for(int i = 0 ; i< m; i++){
      if(chose[i]){
        std::cout << es[i].first << " " << es[i].second << "\n";
      }
    }


  }else{
    std::cout << "No\n";
  }
}

E - Evil Coordinate

机器人从(0,0)(0,0) 出发，地图上在 (mx,my)(m_x,m_y) 位置有地雷。问机器人完成所有指定指令后，是否不会踩到地雷。 所有的指令顺序可以打乱。

思维 模拟

还是挺无脑的暴力的。

一共就 UDLRUDLR 四种移动方式，先完成其中的一种，再完成另一种，如果触碰地雷就将完成循序调换一下，很容易得出结果。

#include<bits/stdc++.h>


int mx, my;
int ex, ey;
std::string route;


void solve() {
    std::cin >> mx >> my >> route;
    ex = ey = 0;
    int op[4] = {0, 0, 0, 0};
    for (int i = 0, len = route.size(); i < len; i++) {
        if (route[i] == 'U') {
            ey++;
            op[0]++;
        } else if (route[i] == 'D') {
            ey--;
            op[1]++;
        } else if (route[i] == 'L') {
            ex--;
            op[2]++;
        } else if (route[i] == 'R') {
            ex++;
            op[3]++;
        }
    }
    if ((ex == mx && ey == my) || (mx == 0 && my == 0)) {
        std::cout << "Impossible\n";
        return;
    }
    std::vector<int> flow = {0, 1, 2, 3};
    bool reachable = false;
    do {
        int x = 0, y = 0;
        for (auto cur_op: flow) {
            if(cur_op == 0){
                // U
                for(int t = 0; t < op[cur_op]; t++){
                    y++;
                    if(x == mx && y == my){
                        goto outter;
                    }
                }
            }else if(cur_op == 1){
                // D
                for(int t = 0; t < op[cur_op]; t++){
                    y--;
                    if(x == mx && y == my){
                        goto outter;
                    }
                }
            }else if(cur_op == 2){
                // L
                for(int t = 0; t < op[cur_op]; t++){
                    x--;
                    if(x == mx && y == my){
                        goto outter;
                    }
                }
            }else if(cur_op == 3){
                // R
                for(int t = 0; t < op[cur_op]; t++){
                    x++;
                    if(x == mx && y == my){
                        goto outter;
                    }
                }
            }
        }
        reachable = true;
        break;


        outter:
        int _unused;
    } while (std::next_permutation(flow.begin(), flow.end()));
    if(reachable){
        for(auto cur_op: flow){
            for(int t = 0; t < op[cur_op]; t++){
                if(cur_op == 0){
                    std::cout << "U";
                }else if(cur_op == 1){
                    std::cout << "D";
                }else if(cur_op == 2){
                    std::cout << "L";
                }else if(cur_op == 3){
                    std::cout << "R";
                }
            }
        }
        std::cout << "\n";
    }else{
        std::cout << "Impossible\n";
    }
}


int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    std::cout.tie(nullptr);


    int t;
    std::cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

F - Fireworks

Kotori nn 分钟能制作一个烟花，每个烟花只有 p×10−4p \times 10^{-4}的可能性成功。当她制作完一个烟花后可以选择再做一个，或者消耗mm分钟将之前制作的烟花燃放。 如果燃放的烟花中有一个成功， Kotori 就会停止燃放，否则她就会继续燃放。求最优策略下塔停止燃放眼花的最小期望时间，

三分 概率

设 Kotori 燃放 kk 次烟花，那么至少一次燃放成功的概率为 1−(1−p)k1- (1-p)^k，其期望为 E(k)=11−(1−p)kE(k)=\frac{1}{1-(1-p)^k}

那么用时期望为 (k×n+m)×E(k)=nk+m1−(1−p)k(k\times n + m) \times E(k) = \frac{nk+m}{1 - (1-p)^k}

之后盲猜这是一个凹函数，用三分法求解:

#include<bits/stdc++.h>


using ld =  double;
using ll =  long;


ld qpow(ld a, ll b)
{
    ld ans = 1;
    ld base = a;
    while(b > 0)
    {
        if(b & 1)
            ans *= base;


        base *= base;
        b >>= 1;
    }
    return ans;
}
ld n, m, p;


ld calc(ll k) {
    return  (k * n + m) / (1 - qpow(1 - p, k));
}


void solve() {
    std::cin >> n >> m >> p;
    p /= 1e4;
    ll l = 1, r = std::numeric_limits<int>::max() / 3 * 2;
    while (l < r) {
        ll mid1 = l + (r - l) / 3;
        ll mid2 = r - (r - l) / 3;
        if(calc(mid1) < calc(mid2)) r = mid2 - 1;
        else l = mid1 + 1;
    }
    std::cout << calc(l) << "\n";
}


int main() {
    int T;
    std::cin >> T;
    std::cout << std::setprecision(5) << std::fixed;
    while (T--) {
        solve();
    }
}

H - Harmonious Rectangle

定义一个和谐矩阵为存在以下任意一种染色的矩阵 1≤x1<x2≤n,1≤y11\le x_1 \lt x_2 \le n, 1 \le y_1

{color(x1,y1)=color(x1,y2)color(x2,y1)=color(x2,y2)或{color(x1,y1)=color(x2,y1)color(x1,y2)=color(x2,y2)\begin{cases} color(x_1, y_1) = color(x_1, y_2) \\\\ color(x_2, y_1) = color(x_2, y_2) \end{cases}\text{或} \begin{cases} color(x_1, y_1) = color(x_2, y_1) \\\\ color(x_1, y_2) = color(x_2, y_2) \end{cases}

输入一个 nn和mm，表示矩阵的长和宽。在上面用红，蓝，黄涂色。输出有多少种染色方式存在和谐矩阵。

结果对 109+710^9 + 7 取模

鸽笼原理 打表

首先当 n=1n=1 或者 m=1m=1 时，根据样例，肯定无解。

当n=2,m=1n=2,m=1时，共有99种组合，也就是说当m>9m\gt9时一定存在和谐矩阵。

进一步推广，也就是当max(n,m)>9max(n,m)\gt 9时一定存在和谐矩阵。我们只需要对max(n,m)≤9max(n,m)\le 9的情况打表即可

然而刚开始没想范围写了个暴力，结果太慢了

正好拿来对拍

def check(map) -> bool:
    for x in range(len(map)):
        for y in range(len(map[x])):


            for w in range(x+1, len(map)):
                for h in range(y+1, len(map[x])):


                    if map[x][y] == map[w][y] and map[x][h] == map[w][h]:
                        return True
                    elif map[x][y] == map[x][h] and map[w][y] == map[w][h]:
                        return True
    return False


map = [[None for i in range(9)] for j in range(9)]


def zero(n, m):
    return [[0 for i in range(n)] for j in range(m)]


def is_end(map) -> bool:
    for y in map:
        for x in y:
            if x != 2:
                return False
    return True


def inc(map):
    map[0][0] += 1
    for i in range(len(map)):
        for j in range(len(map[i])):
            if map[i][j] > 2:
                map[i][j] = 0
                if j+1 == len(map[i]):
                    if i+1 != len(map):
                        map[i+1][0] += 1
                else:
                    map[i][j+1] += 1


with open("H.txt", "w") as f:
    f.write("{")
    for m in range(1, 10):
        f.write("{")
        for n in range(1, 10):
            ans = 0
            map = zero(n, m)
            print(str(len(map)) + "," + str(len(map[0])))
            if check(map):
                ans += 1
            while True:
                inc(map)
                if check(map):
                    ans += 1
                if is_end(map):
                    break
            print(ans)
            f.write(str(ans))
            if n != 9:
                f.write(",")
        if m != 9:
            f.write(",")
        f.write("}")

修改之后成了这样子：

#include <bits/stdc++.h>


const int MODD = 1e9 + 7;
const int MAXN = 12;
using ll = long long;


template <typename A, typename BaseT>
typename std::enable_if<std::is_integral<BaseT>::value, A>::type
qpow(A a, BaseT n, BaseT modd) {
  decltype(a) ans = 1;
  while (n) {
    if (n & 1)
      ans = (ans * a) % modd;
    n >>= 1;
    a = (a * a) % modd;
  }
  return ans % modd;
}


int a[MAXN][MAXN];
int m, n;
ll gcnt;


void dfs(int xx, int yy) {
  for (int color = 0; color < 3; color++) {
    int x2 = xx;
    int y2 = yy;
    a[y2][x2] = color;
    bool flag = true;
    for (int y1 = 0; y1 < y2 && flag; y1++) {
      for (int x1 = 0; x1 < x2 && flag; x1++) {
        if ((a[y1][x1] == a[y2][x1] && a[y1][x2] == a[y2][x2]) ||
            (a[y1][x1] == a[y1][x2] && a[y2][x1] == a[y2][x2])) {
          flag = false;
          gcnt += qpow(3LL, (n - 1 - y2) * m + (m - 1) - x2, MODD);
          gcnt %= MODD;
        }
      }
    }
    if (flag) {
      x2++;
      if (x2 >= m) {
        x2 = 0;
        y2++;
        if (y2 >= n) {
          continue;
        }
      }
      dfs(x2, y2);
    }
  }
  a[yy][xx] = -1;
}


int solve() {
  gcnt = 0;
  dfs(0, 0);
  return gcnt;
}


int main() {
  std::ofstream os("H.txt");


  for (n = 1; n <= 9; n++) {
    os << "{";
    for (m = 1; m <= 9; m++) {
      std::cout << n << "x" << m << "\n";
      if (std::min(n, m) == 1) {
        os << 0 << ",";
        continue;
      } else {
        std::memset(a, 0, sizeof(a));
        os << solve();
        if (m != 9) {
          os << ",";
        }
      }
    }
    os << "}";
    if (n != 9) {
      os << ",\n";
    }
  }
}

AC 代码:

#include <bits/stdc++.h>


template<typename A, typename BaseT>
typename std::enable_if<std::is_integral<BaseT>::value, A>::type
qpow(A a, BaseT n, BaseT modd){
    decltype(a) ans = 1;
    while (n){
        if (n & 1) ans = (ans * a) % modd;
        n >>= 1;
        a = (a * a) % modd;
    }
    return ans % modd;
}


using ll = long long;
int map[][9] = {
{0,0,0,0,0,0,0,0,0,},
{0,15,339,4761,52929,517761,4767849,43046721,387420489},
{0,339,16485,518265,14321907,387406809,460338013,429534507,597431612},
{0,4761,518265,43022385,486780060,429534507,792294829,175880701,246336683},
{0,52929,14321907,486780060,288599194,130653412,748778899,953271190,644897553},
{0,517761,387406809,429534507,130653412,246336683,579440654,412233812,518446848},
{0,4767849,460338013,792294829,748778899,579440654,236701429,666021604,589237756},
{0,43046721,429534507,175880701,953271190,412233812,666021604,767713261,966670169},
{0,387420489,597431612,246336683,644897553,518446848,589237756,966670169,968803245}
};
#define int ll


const int modd = 1e9 + 7;
void solve() {
  int n, m;
  std::cin >> n >> m;
  if (n > m)
    std::swap(n, m);
  if(n == 1) {
    std::cout << 0 << "\n";
    return;
  }
  if(m > 9){
    int result = qpow(3LL, n * m, modd);
    std::cout << result << "\n";
  }else{
    std::cout << map[n-1][m-1]%modd << "\n";
  }
}


#undef int
int main() {
  std::ios::sync_with_stdio(false);
  std::cin.tie(nullptr);
  std::cout.tie(nullptr);


  int T;
  std::cin >> T;
  while (T--) {
    solve();
  }
}

K - K Co-prime Permutation

kk co-prime 排列是指排列中有 kk 个数字 aia_i 和 ii 互质。

输入序列长度 nn 和 kk, 构造这样的排列

思维 签到

一个数和他相邻的数互质，我们只需要将kk个数错开一位就行。

直接调库

#include <bits/stdc++.h>


int main() {
#define int long long
    int n, k;
    std::cin >> n >> k;
    if(k == 0) {
        std::cout << -1;
        return 0;
    }
    if(n == 1){
        std::cout << 1;
        return 0;
    }
    std::vector<int> seq(n);
    for(int i = 0; i < n; i++){
        seq[i] = i+1;
    }
    std::rotate(seq.begin(), seq.begin() + 1, seq.end() - (n-k));
    for(int i = 0; i < n ; i++){
        std::cout << seq[i] << " ";
    }


    return 0;
}

L - Let’s Play Curling

红队 n 个冰壶、蓝队 m 个冰壶，给出所有冰壶的坐标，找到一个位置 c 使得红队能赢且得分尽可能多，若红队能赢输出最多能得到的分数，若红队不能赢输出 Impossible。

思维

红队得分的条件是红队的冰壶离中心点cc比蓝队近，所以这个题可以转化成任意相邻的两个烂队冰壶之间最多有几个红队的冰壶。

// clang-format off
#include <bits/stdc++.h>


using ll = long long;
using ul = unsigned long long;
using ld = long double;


template<typename T>
inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x) {
    char c;
    T f = 1;
    while (!isdigit(c = getchar())) if (c == '-')f = -1;
    x = (c & 15);
    while (isdigit(c = getchar())) x = (x << 1) + (x << 3) + (c & 15);
    x *= f;
}


template<typename T, typename... A>
inline void read(T &value, A &..._t) { read(value), read(_t...); }


void solve(const std::size_t testcase);


#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)
#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)
#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)
#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)


int main() {
    std::size_t t = 1;
    read(t);
    // std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr);
    rep1(i, t) solve(t);
    return 0;
}
// clang-format on
#define int ll


const int INF = std::numeric_limits<int>::max();


const int maxn = 1e5 + 17;
int n, m;
int blue[maxn], red[maxn];


void solve(const std::size_t testcase) {
    read(n, m);
    rep1(i, n) read(red[i]);
    rep1(i, m) read(blue[i]);
    std::sort(red + 1, red + n + 1);
    std::sort(blue + 1, blue + m + 1);
    blue[m + 1] = INF;
    ll ans = 0;
    rep(i, m + 1) {
        int l = std::upper_bound(red + 1, red + n + 1, blue[i]) - (red + 1) + 1;
        int r = std::lower_bound(red + 1, red + n + 1, blue[i + 1]) - (red + 1) + 1 - 1;
        if (red[l] <= blue[i] || red[r] >= blue[i + 1]) continue; // for duplicated element
        ans = std::max(ans, r - l + 1);
    }
    if (ans != 0) {
        std::cout << ans << "\n";
    } else {
        std::cout << "Impossible\n";
    }
}

M - Monster Hunter

在一个根节点为 11 的有nn个定点的有根树，每个顶点都有一个怪物，第ii个顶点上的怪物有hpihp_i滴血。现在要按照下列规则杀死所有怪物

  • 当一个顶点的直接父节点上的怪物被杀死时，这个节点上的怪物才能被杀死
  • 杀死第 ii 个节点上的怪物需要消耗的能量为第ii个节点上的怪物hpihp_i和这个节点的所有直接子节点上的存活的怪物的hphp总和，即消耗的能量为
hpi+∑顶点j上的怪物是存活状态且i的直接子节点是jhpjhp_i + \sum_{\begin{array}{c}\text{顶点} j \text{上的怪物是\textbf{存活}状态} \\\\ \text{且} i \text{的直接子节点是} j \end{array}} hp_j
  • 使用魔咒消耗00能量，且无视上述限制，杀死选择的怪物。

当符卡数量 m=0,1,2,…,nm=0,1,2,\ldots,n 时，输出杀死所有怪物所需消耗的最小能量

树形背包

很喜欢yrh说过的一句话，“不会dp”

一开始想着倒着进行贪心，贪着贪着就挂了。

正解是 dp，某种意义上还挺好理解。dp[i][j][k]dp[i][j][k]，其中ii表示当前节点的编号，jj表示使用的魔咒的数量，kk表示是否选择当前节点。

转移方程为

{dp[i][j][0]=dp[i][j−k][0]+min⁡(dp[son][k][0],dp[i][j−k][1])dp[i][j][1]=dp[i][j−k][1]+min⁡(dp[son][k][0],dp[son][k][1]+hp[son])\begin{cases} dp[i][j][0]=dp[i][j-k][0]+\min(dp[son][k][0], dp[i][j-k][1])\\\\ dp[i][j][1]=dp[i][j-k][1]+\min(dp[son][k][0], dp[son][k][1]+hp[son]) \end{cases}

对于第二维，我们可以使用滚动数组消掉实测不消也能过

#include <bits/stdc++.h>


template <typename T>
inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x) {
  char c;
  T f = 1;
  while (!isdigit(c = getchar()))
    if (c == '-')
      f = -1;
  x = (c & 15);
  while (isdigit(c = getchar()))
    x = (x << 1) + (x << 3) + (c & 15);
  x *= f;
}
template <typename T, typename... A> inline void read(T &value, A &..._t) {
  read(value), read(_t...);
}


using ll = long long;


const int maxn = 2021;
const int maxm = 1e5 + 17;
const ll INF = (1ll << 60);


struct edge {
  int next, to;
} e[maxm];


int head[maxn], idx = 0;


void add_edge(int x, int y) {
  e[++idx].next = head[x];
  head[x] = idx;
  e[idx].to = y;
}


int n;


int hp[maxn], size[maxn];
ll dp[maxn][maxn][2];
ll temp[maxn];


void dfs(int x){
  for(int i = 0; i <=n; i++){
    dp[x][i][0] = dp[x][i][1] = INF;
  }
  dp[x][0][1] = hp[x];
  dp[x][1][0] = 0;
  size[x] = 1;
  for(int i = head[x]; i != 0; i = e[i].next){
    const int v = e[i].to;
    dfs(v);


    for(int j = 0 ; j <= size[x] + size[v]; j++){
      temp[j] = INF;
    }


    for(int j = 0; j <= size[x]; j++){
      for(int k = 0; k <= size[v]; k++){
        temp[j+k] = std::min(temp[j+k], dp[x][j][0] + std::min(dp[v][k][0], dp[v][k][1]));
      }
    }


    for(int j = 0; j <= size[x] + size[v]; j++){
      dp[x][j][0] = temp[j];
      temp[j] = INF;
    }


    for(int j = 0; j <= size[x]; j++){
      for(int k = 0; k <= size[v]; k++){
        temp[j+k] = std::min(temp[j+k], dp[x][j][1] + std::min(dp[v][k][0], dp[v][k][1] + hp[v]));
      }
    }
    for(int j = 0; j <= size[x] + size[v]; j++){
      dp[x][j][1] = temp[j];
      temp[j] = INF;
    }
    size[x] += size[v];
  }
}


void solve() {
  read(n);
  for(int i = 2; i <= n; i++){
    int p;
    read(p);
    add_edge(p, i);
  }
  for(int i = 1; i <= n; i++){
    read(hp[i]);
  }
  dfs(1);
  for(int i = 0; i <= n; i++){
    std::cout << std::min(dp[1][i][0], dp[1][i][1]) << " ";
  }
  std::cout << std::endl;


  std::memset(head, 0, sizeof(head));
  idx = 0;
}


int main() {
  int T;
  read(T);
  while (T--) {
    solve();
  }
}
moe-counter

统计自 2024 年 9 月