Codeforces Round 894 (Div. 3) A-G

发布于 2023-08-25 # Competitive Programming # Codeforces

A. Gift Carpet

输入一个 $n$ 行 $m$ 列的字符矩阵，判断矩阵中从前往后的列中能不能找到特定的字符组成 vika

暴力

直接旋转矩阵然后暴力判断 :)

T = int(input())

def solve():
  r, c = list(map(int, input().split()))
  s = [input() for i in range(r)]
  s[::] = [[row[i] for row in s[::-1]] for i in range(len(s[0]))]
  s = ["".join(i) for i in s]
  v, vi, vik, vika = [False, False, False, False]

  for line in s:
    if vik and 'a' in line:
      vika = True
    if vi and 'k' in line:
      vik = True
    if v and 'i' in line:
      vi = True
    if 'v' in line:
      v = True

  print("YES" if vika else "NO")
while T != 0:
  T -= 1
  solve()

B. Sequence Game

已知 $a$ 序列可以通过特定的规则变化成 $b$ 序列，规则如下：

将 $a_1$ 加入序列 $b$

当 $a_i \ge a_{i-1}\quad(2 \le i \le m)$ 时，将 $a_i$ 加入序列 $b$

比如 $[4,3,2,6,3,3]$ 变化为 $[4,6,3]$

现给出长度为 $n$ 的序列 $b$ ，请构造出符合上述条件的序列 $a$ ，长度不能超过 $2n$

构造

题目要进行一个逆向恢复的过程，由于题目要求构造的序列长度不能超过 $2n$ ，先粗略考虑将 $b$ 中的每 $1$ 个元素变成 $a$ 中的 $2$ 个元素。当构造的两个元素相同时，后一个元素 $a_j$ 一定会被添加到 $b$ ，而前一个元素当大于等于前一个元素时也可能会被添加到 $b$ 中。出现第二种情况时， $a_j$ 就没有必要了。

因此我们可以整理出以下思路：

若 $b_i \ge last(a)$ 或 $a$ 为空，将一个 $b_i$ 添加到 $a$ 中
若 $b_i < last(a)$ ，则将两个 $b_i$ 添加到 $a$ 中

T = int(input())

def solve():
  n = int(input())
  b = list(map(int, input().split()))
  a = []
  for i in range(n):
    if i == 0 or b[i] >= b[i-1]:
      a.append(b[i])
    else:
      a.extend([b[i], b[i]])
  print(len(a))
  print(" ".join(map(str, a)))

while T != 0:
  T -= 1
  solve()

C. Flower City Fence

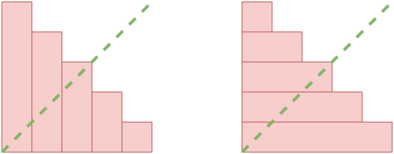
输入 $n$ 个数 $a$ ，每个 $a_i$ 表示高度， $n$ 表示宽度，形成一个类似条形图的图形。

问该图形是否沿直线 $x=y$ 对称

暴力

不太清楚为什么 CF 的标签上会有二分和排序

实际上只需要遍历每个块，判断第 $i$ 个块是否满足第 $i$ 个块的高度 $a[i]$ 与 $j$ 相等（其中 $j$ 为第一个 $a[j] >= i$ 的值）

~~写 GO 语言不用读入优化会 TLE on 6~~

~~狗都不写 GO~~

package main

import (
    "bufio"
    "fmt"
    "os"
    "strconv"
    "strings"
)

func solve(in *bufio.Reader) {
    n := readInt(in)
    a := readArrInt(in)
    alen := n
    for i := 0; i < n; i++ {
        for alen > 0 && a[alen-1] <= i {
            alen--
        }
        if a[i] != alen {
            fmt.Println("NO")
            return
        }
    }
    fmt.Println("YES")
}
func main() {
    in := bufio.NewReader(os.Stdin)
    T := readInt(in)

    for i:= 0; i < T; i++ {
        solve(in)
    }
}

func readInt(in *bufio.Reader) int {
    nStr, _ := in.ReadString('\n')
    nStr = strings.ReplaceAll(nStr, "\r", "")
    nStr = strings.ReplaceAll(nStr, "\n", "")
    n, _ := strconv.Atoi(nStr)
    return n
}

func readLineNumbs(in *bufio.Reader) []string {
    line, _ := in.ReadString('\n')
    line = strings.ReplaceAll(line, "\r", "")
    line = strings.ReplaceAll(line, "\n", "")
    numbs := strings.Split(line, " ")
    return numbs
}

func readArrInt(in *bufio.Reader) []int {
    numbs := readLineNumbs(in)
    arr := make([]int, len(numbs))
    for i, n := range numbs {
        val, _ := strconv.Atoi(n)
        arr[i] = val
    }
    return arr
}

D. Ice Cream Balls

Tema 正在制作双球冰激凌。现在要制作 $m$ 种不同的冰激凌，最少需要几个球？球的种类可以不同，并且有无限多种

注意：不同种类球的放置顺序与产物的种类无关，即 $\\{1,2\\}= \\{2,1\\}$ ，但 $\\{1,1\\} \ne \\{1, 2\\}$

组合数学 二分答案

极限情况下，可以每个雪糕球的种类都不相同，这样每取两个就可以形成一种冰激凌，可以保证取到的双球冰激凌种类最多。在这种情况下，每添加一个雪糕球之前已经存在过，那么双球冰激凌种类就会加一。

那么我们可以二分雪糕球的种类 $k$ ，每次 check $k$ 种雪糕球能形成的双球冰激凌的种类 $\frac{C_n^2 C_{n-2}^2C_{n-4}^2 \ldots C^2_2}{A^\frac{n}{2}_\frac{n}{2}}=C_n^2$ 和 $m$ 的关系，保证 $C_n^2 \le m$ ，最终答案即为 $n + (m - C^2_n)$

int C2(int n){
  return (n * (n-1))/2;
}

void solve() {
  int n;
  read(n);
  int L = 1, R = 2648956421;
  while(L < R){
    int mid = L + (R - L + 1) / 2;
    if(C2(mid) <= n) L = mid;
    else R = mid - 1;
  }
  std::cout << L + (n - C2(L));
}

根据此其实可以给出一个非二分的写法

若最终有 $m$ 种，则在最优情况下应该是使用了都不相同的雪糕球时 $C_n^2 = \frac{n(n-1)}{2} = m$

那么 $n-1 \le \sqrt{2m} \le n$

令 $i = \sqrt{2m}$ ，我们只需要尽可能的使 $i \to n$ ，也就是满足 $i(i-1) <= 2n$ 时尽可能大

use std::io;

fn solve() {
    let mut input = String::new();
    io::stdin().read_line(&mut input).unwrap();
    let n: i64 = input.trim().parse().unwrap();

    let mut i = ((2 * n) as f64).sqrt() as i64;
    while i * (i - 1) <= 2 * n {
        i += 1;
    }
    if i * (i - 1) > 2 * n {
        i -= 1;
    }
    print!("{}\n", i + (n - i * (i - 1)/ 2));
}

fn main() {
    let mut input = String::new();
    io::stdin().read_line(&mut input).unwrap();
    let t: i64 = input.trim().parse().unwrap();
    for _ in 0..t {
        solve();
    }
}

E. Kolya and Movie Theatre

影院在 $n$ 天中每天放一部新电影。每部电影都有一个价值 $a_i$

当 Kolya 不去看某电影时，下一部电影的价值将下降 $d \cdot cnt$ ，其中 $d$ 代表预定值， $cnt$ 表示距离上次看电影过了几天。

Kolya 最多只能看 $m$ 次电影，制定一个计划，使 Kolya 的观影价值最大

贪心

如果我们选择 $1,3$ 的电影，答案为 $a_1 - (1-0)d + a_3 - (3-1)d = a_1 +a_3 - 3d$

如果我们选择 $1,2,4$ 的电影，答案为 $a_1 - (1-0)d + a_2 - (2-1)d + a_4 - (4-2)d = a_1 + a_2 + a_4 + 4d$

也就是说无论 Kolya 选择看哪几天的电影，只要最后选择第 $k$ 天的电影，那么价值下降的总和都是 $kd$ ，完整的答案为

\sum_{i \in S} a_i - \max_{i \in S}(i)\times d

用优先队列去枚举最大的 $S$ 集合即可

void solve() {
  int n, m, d;
  read(n, m, d);
  std::vector<int> a(n+1);
  reads(all1(a));

  int max = 0;
  int ans = 0;
  std::priority_queue<int, std::vector<int>, std::greater<>> q;

  for(int i = 1; i <= n; i++){
    if(a[i] < 0) continue;
    ans += a[i];
    q.push(a[i]);
    if(q.size() > m){
      ans -= q.top();
      q.pop();
    }
    max = std::max(max, ans - i * d);
  }
  std::cout << max;
}

F. Magic Will Save the World

Vika 有水魔法和火魔法，每秒钟 Vika 可以产生 $w$ 单位水魔力和 $f$ 单位火魔力。施展魔法需要魔力，而刚开始 Vika 没有任何魔力。

现在有 $n$ 只怪物，击败每个怪物需要使用消耗 $s_i$ 魔力的魔法。

Vika 可以在一秒中内无限使用魔法，请求出消灭所有怪物至少需要多少秒

子集枚举

看到这个问题首先想到的是 dp

f[i][j][k] = max(f[i-1][j][k] , f[i-1][j-s[i]][k] + 1, f[i-1][j][k-s[i]]+1)

但是受限于数据范围 $1 \le w, f \le 10^9$ 这样肯定不可行

考虑列出所有怪物血量可组成的集合的子集，枚举子集 $i$ ，计算使用火魔法消灭 $i$ 使用水魔法消灭 $sum - i$ 所需要的时间，统计最小值

const int maxs = 1e4 * 100 + 17;
void solve() {
  int w, f, n;
  read(w, f, n);
  std::vector<int> s(n + 1);
  reads(all1(s));

  std::bitset<maxs> dp;
  dp[0] = 1;
  int sum = 0;
  for (int i = 1; i <= n; i++) {
    dp |= dp << s[i];
    sum += s[i];
  }

  int ans = 1e9;
  for (int i = 0; i <= sum; i++) {
    if (dp[i]) {
      int t = std::max(std::ceil(1.0 * i / w), std::ceil(1.0 * (sum - i) / f));
      ans = std::min(ans, t);
    }
  }
  std::cout << ans;
}

G. The Great Equalizer

现有一均衡器设备接受数组 $a$ 作为输入。均衡器将会：

升序排序并去重

如果当前数组的长度为 $1$ ，均衡器将停止工作，并将数组中唯一的元素作为设备输出

在数组中的每个元素加上等差数列 $\\{n - 0, n - 1, n -2, \ldots, 1\\}$ 中对应的元素，其中 $n$ 表示数组长度。即索引从 $0$ 开始时，令第 $i$ 个元素为 $a[i] + (n-i)$

为了测试设备，将一个数组 $a$ 作为输入，并进行 $q$ 次操作：

将 $x$ 赋值给指定元素 $a_i$

将数组 $a$ 作为设备的输入，并记录设备的输出。数组 $a$ 在设备运行中保持不变

找出设备每次操作后的输出值

稍微玩一玩样例，可以发现每次操作都可以将两个相邻的两个数的差减小 $1$ 。也就是说将数组变为相同的一个数需要 $t=\max_{2 \le i\le n}(a[i] - a[i-1])$ 次操作。最终剩余的数一定是最大的数 $a[n] + t$

比如 $[1,6,10]$ ，相邻的两个数最大差 $6-1=5$ ，答案即为 $10 + 5 = 15$

直接白嫖 std::multiset 维护集合和相邻两个数的差，每次维护操作复杂度 $O(\log n)$

void solve() {
    int n;
    std::cin >> n;

    std::vector<int> a(n);
    for (int i = 0; i < n; i++) {
        std::cin >> a[i];
    }

    std::multiset<int> s, d{0};

    auto add = [&](int x) {
        auto it = s.insert(x);
        auto r = std::next(it);
        if (it != s.begin()) {
            d.insert(x - *std::prev(it));
        }
        if (r != s.end()) {
            d.insert(*r - x);
        }
        if (it != s.begin() && r != s.end()) {
            d.extract(*r - *std::prev(it));
        }
    };

    auto del = [&](int x) {
        auto it = s.find(x);
        auto r = std::next(it);
        if (it != s.begin()) {
            d.extract(x - *std::prev(it));
        }
        if (r != s.end()) {
            d.extract(*r - x);
        }
        if (it != s.begin() && r != s.end()) {
            d.insert(*r - *std::prev(it));
        }
        s.erase(it);
    };

    for (int i = 0; i < n; i++) {
        add(a[i]);
    }

    int q;
    std::cin >> q;
    for (int i = 0; i < q; i++) {
        int x, y;
        std::cin >> x >> y;
        x--;
        del(a[x]);
        a[x] = y;
        add(a[x]);
        int ans = *s.rbegin() + *d.rbegin();
        std::cout << ans << " "[i == q - 1];
    }
}

Mslxl's Blog

Integrate Life