Codeforces Round 841 (Div. 2) and Divide by Zero 2022 - ABCD
Codeforces Round #841 (Div. 2) and Divide by Zero 2022
A - Joey Takes Money
给一个长度为 n 的整数序列
选择两个数 和 ,将其替换为 , ,其中 x _ y = a_i _ a_j ,这个操作可以进行无数次
输出这个序列的和乘以
直接暴力就行:
// clang-format off#include <bits/stdc++.h>#include <functional>using ll = long long; using ul = unsigned long long; using ld = long double;template <typename T> inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x){ char c;T f=1; while(!isdigit(c=getchar())) if(c=='-')f=-1; x=(c&15); while(isdigit(c=getchar())) x= (x<<1) + (x<<3) + (c&15); x*=f; } template <typename T, typename... A> inline void read(T &value, A &..._t) { read(value), read(_t...); }void solve(const std::size_t testcase);#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)int main() { std::size_t t = 1; read(t); rep1(i, t) solve(t); return 0;}// clang-format on
// coding here#define int ulvoid solve(const std::size_t testcase) { int n; read(n);
std::vector<int> seq(n); rep(i, n) read(seq[i]); if (n == 1) { std::cout << seq[0] * 2022<< std::endl; return; } std::sort(seq.begin(), seq.end());
for (int i = 0; i < n - 1; i++) { seq[i+1] = seq[i] * seq[i+1]; seq[i] = 1; } std::cout << ((n-1) + seq[n-1]) * 2022<< std::endl;}B - Kill Demodogs
一个矩阵,从 出发走到 ,每经过可得分。 只能向下或者向右走
问全程最大积分是多少?
首先根据 ,当 时,取最大,所以移动路线应该是这样的:
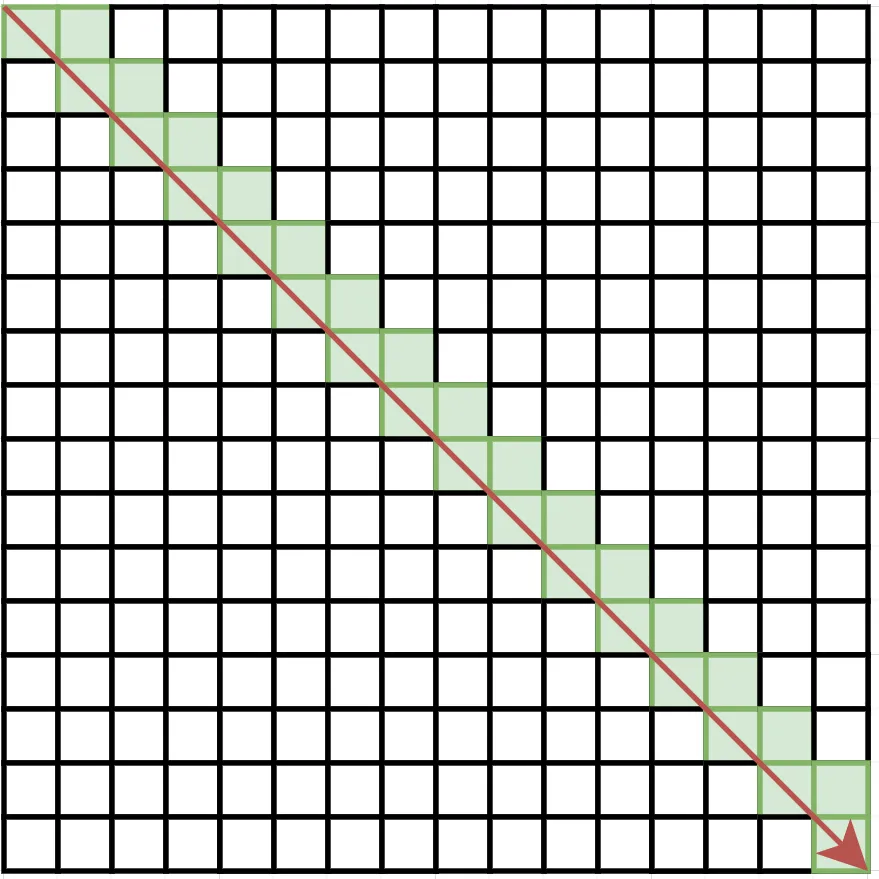
当我们走到时,获得积分
从第一行走第二行,获得积分
以此类推,当我们走完 行时,获得积分
走到 ,即求数列 前 项的和
本来当存在取模时,除法要求逆元,但是正好题目要求答案乘以 2022,所以最终答案是
// clang-format off#include <bits/stdc++.h>using ll = long long; using ul = unsigned long long; using ld = long double;void solve(const std::size_t testcase);#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)int main() { std::ios::sync_with_stdio(false); std::cout.tie(nullptr); std::cin.tie(nullptr); std::size_t t = 1; std::cin >> t; rep1(i, t) solve(t); return 0;}// clang-format onconst ul modd = 1e9 + 7;
// coding herevoid solve(const std::size_t testcase) { ul n; std::cin >> n; ll ans = n * (4 * n - 1) % modd * (n + 1) % modd ; ans = ans % modd * 337 % modd; std::cout << ans << "\n";}C - Even Subarrays
给一段长度为 n 的序列 ,从中找到他的连续子序列,并且这个连续子序列的因数个数为偶数。
问这样的子序列个数为多少
首先一个数的因子都是成对出现的,当这个数是平方数的时候会出现两个一样的因子,也就是说当 一个数不是平方数的时候,它的因子个数一定是偶数个。
因此我们只需要判断有多少个子区间的异或和为平方数,最后用子区间的个数减去子区间中异或和为平方数的个数即可。
这个统计操作有一个相似的题目: Crazy Binary String,
// clang-format off#include <bits/stdc++.h>using ll = long long; using ul = unsigned long long; using ld = long double;template <typename T> inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x){ char c;T f=1; while(!isdigit(c=getchar())) if(c=='-')f=-1; x=(c&15); while(isdigit(c=getchar())) x= (x<<1) + (x<<3) + (c&15); x*=f; } template <typename T, typename... A> inline void read(T &value, A &..._t) { read(value), read(_t...); }void solve(const std::size_t testcase);#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)int main() { std::size_t t = 1; read(t); // std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr); rep1(i, t) solve(t); return 0;}// clang-format on#define int ll
void solve(const std::size_t testcase) { int n; read(n); std::vector<int> a(n + 1); rep1(i, n) { read(a[i]); a[i] ^= a[i - 1]; } std::vector<int> mp(4 * n); int ans = 0; mp[0] = 1; rep1(i, n) { for (int x = 0; x * x <= 2 * n; x++) { int num = x * x; ans += mp[a[i] ^ num]; } mp[a[i]]++; } std::cout << ll(n * (n + 1) / 2) - ans << "\n";}D - Valiant’s New Map
二分+二维前缀和
应该有别的思路
题目给一个 的矩阵,从里面选择 的子矩阵,并且这个子矩阵的元素最小值必须不小于
从 中二分 ,check函数用二维前缀和即可。
能卡着时间跑过。
#include <bits/stdc++.h>using ll = long long; using ul = unsigned long long; using ld = long double;template <typename T> inline typename std::enable_if<std::is_integral<T>::value>::type read(T &x){ char c;T f=1; while(!isdigit(c=getchar())) if(c=='-')f=-1; x=(c&15); while(isdigit(c=getchar())) x= (x<<1) + (x<<3) + (c&15); x*=f; } template <typename T, typename... A> inline void read(T &value, A &..._t) { read(value), read(_t...); }void solve(const std::size_t testcase);#define rep(NAME, MAX) for(decltype(MAX) NAME = 0; NAME < MAX; NAME++)#define rep1(NAME, MAX) for(decltype(MAX) NAME = 1; NAME <= MAX; NAME++)#define repv0(NAME, START) for(decltype(START) NAME = START; NAME >= 0; NAME--)#define repv1(NAME, START) for(decltype(START) NAME = START; NAME >= 1; NAME--)int main() { std::size_t t = 1; read(t); // std::ios::sync_with_stdio(false); std::cin.tie(nullptr); std::cout.tie(nullptr); rep1(i, t) solve(t); return 0;}// clang-format onbool check(int k, const std::vector<std::vector<int>> &a, ll n, ll m) { std::vector<std::vector<int>> pre(n + 1, std::vector<int>(m + 1, 0)); for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { pre[i][j] = (a[i][j] >= k) + pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1]; } } for (int i = k; i <= n; i++) { for (int j = k; j <= m; j++) { int x = i - k + 1, y = j - k + 1; if (pre[i][j] + pre[x - 1][y - 1] - pre[x - 1][j] - pre[i][y - 1] == k * k) return true; } } return false;}
void solve(const std::size_t testcase) { ll n, m; read(n, m); std::vector<std::vector<int>> mp(n + 1, std::vector<int>(m + 1)); rep1(i, n) { rep1(j, m) { read(mp[i][j]); } } int r = std::min(n, m); int l = 1; int ans = 0; while (l <= r) { int mid = l + (r - l) / 2; if(check(mid, mp, n,m)){ ans = std::max(ans, mid); l = mid + 1; }else{ r = mid - 1; } } std::cout << ans << std::endl;}